Reglas básicas de integración
Derivada de
una función:
Se define como la razón de
cambio de la variable dependiente respecto a la variable independiente.
Las derivadas de las
diferentes funciones básicas son:
la derivada de una
constante,la derivada de una función idéntica,la derivada de una suma y
diferencia de dos funciones,la derivada del producto de dos funciones,la
derivada del cociente de dos funciones y la derivada de una potencia.
Derivada de
una constante:
La derivada de una
constante se define como igual a cero.
y=k
Derivada de
una función identica:
La derivada de una funcion
identica se define como igual a uno.
y=x
Derivada de la
suma y diferencia de dos funciones:
se define como la derivada
de la suma y la diferencia de la dos funciones.
Derivada del
producto de dos funciones:
Es igual a la primera
función multiplicada por la derivada de la segunda función más la segunda
función multiplicada por la derivada de la primera función.
Derivada del
cociente de dos funciones:
Es igual a el denominador
multiplicado por la derivada del numerador menos el numerador multiplicado por
la derivada del denominador, todo esto dividido entre el denominador elevado al
cuadrado.
Derivada de
una potencia:
Es igual al numero que
corresponde al exponente multiplicado por la función elevada al exponente
disminuido en uno.
Una de las muchas
aplicaciones de las derivadas es que la derivada geometricamente representa la
pendientes de una función
Definición de
recta tangente con pendiente m:
Si f está definida en un intervalo abierto que contiene a c y además existe el límite
entonces ,la recta que pasa por (c,f(c)) y cuenta con la pendiente m es la recta tangente de f en el punto (c,f(c)).
Ejemplo:
Calcular las pendientes de las rectas tangente a la gráfica de
f(x) = x2 + 1 en los puntos (0,1) y (-1,2) y representarlos en una gráfica.
Solución:
Utilizando las reglas básicas de derivación tenemos que
f′(x)=d[x2]dx+d[1]dx=2xf′(x)=d[x2]dx+d[1]dx=2x
f′(x)=2xf′(x)=2x
f′(0)=2(0)=0f′(0)=2(0)=0
f′(−1)=2(−1)=−2f′(−1)=2(−1)=−2
Las gráficas de las rectas que tienen esta pendiente son:
Si f está definida en un intervalo abierto que contiene a c y además existe el límite

entonces ,la recta que pasa por (c,f(c)) y cuenta con la pendiente m es la recta tangente de f en el punto (c,f(c)).
Ejemplo:
Calcular las pendientes de las rectas tangente a la gráfica de
f(x) = x2 + 1 en los puntos (0,1) y (-1,2) y representarlos en una gráfica.
Solución:
Utilizando las reglas básicas de derivación tenemos que
f′(x)=d[x2]dx+d[1]dx=2xf′(x)=d[x2]dx+d[1]dx=2x
f′(x)=2xf′(x)=2x
f′(0)=2(0)=0f′(0)=2(0)=0
f′(−1)=2(−1)=−2f′(−1)=2(−1)=−2
Las gráficas de las rectas que tienen esta pendiente son:
Para saber más sobre
derivación haga clic aquí en:
derivada
Criterio de la primera derivada .
Derivada de una potencia
Cálculo integral:
La integración de define como la operación inversa o contraria a la derivación,a la integración es llamada muchas veces antiderivada.
La integración se representa por el símbolo ∫ que es un s alargada
esta notación fue utilizada por primera vez por LEIBNITZ,otra notación que se utilizaba era A(x) que significa antiderivada.
De manera que la integral de una función f(x) es otra función p(x).
La función que se obtiene como resultado de integral f(x) es conocida como función primitiva de f(x).
Ejemplo las funciones primitivas de f(x) = x4son:
Esta son primitiva ya que cuando derivamos cada una de estas funciones nos da como resultado x4x4
derivada
Criterio de la primera derivada .
Derivada de una potencia
Cálculo integral:
La integración de define como la operación inversa o contraria a la derivación,a la integración es llamada muchas veces antiderivada.
La integración se representa por el símbolo ∫ que es un s alargada
esta notación fue utilizada por primera vez por LEIBNITZ,otra notación que se utilizaba era A(x) que significa antiderivada.
De manera que la integral de una función f(x) es otra función p(x).
La función que se obtiene como resultado de integral f(x) es conocida como función primitiva de f(x).
Ejemplo las funciones primitivas de f(x) = x4son:
Esta son primitiva ya que cuando derivamos cada una de estas funciones nos da como resultado x4x4
Integral indefinida:
Como se acaba de ver cada una de las funciones anteriores tienen como derivada f(x) = x4 , esto significa que esta tiene varias funciones primitivas ,y esta solo difieren en una constante C.
La constante C, la cual no es una constante definida al obtener la primitiva de la función,por esta razón a estas integrales se le conoce como indefinidas.






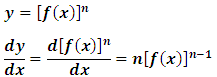

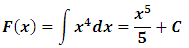

Gracias por el aporte :)
ResponderBorrarBien
ResponderBorrarExcelente información gracias
ResponderBorrar