PROPIEDADES DE LA INTEGRAL DEFINIDA
Se enuncian algunas propiedades y teoremas básicos
de las integrales definidas que ayudarán a evaluarlas con más facilidad.
2) Si f y g son integrables
en [a, b] y c es una constante, entonces las siguientes propiedades son
verdaderas:
(se pueden generalizar para más de dos
funciones)
5) Propiedad de aditividad del intervalo: si f
es integrable en los dos intervalos cerrados definidos por a, b y c entonces 



INTENTE DEMOSTRAR LAS PROPIEDADES
ENUNCIADAS
|
CONSERVACIÓN DE DESIGUALDADES
Demostración: Si
f(x) 0 entonces  representa
el área bajo la curva de f de modo que la interpretación geométrica de esta
propiedad es sencillamente el área. (También se deduce directamente de la
definición porque todas las cantidades son positivas).
representa
el área bajo la curva de f de modo que la interpretación geométrica de esta
propiedad es sencillamente el área. (También se deduce directamente de la
definición porque todas las cantidades son positivas).
 representa
el área bajo la curva de f de modo que la interpretación geométrica de esta
propiedad es sencillamente el área. (También se deduce directamente de la
definición porque todas las cantidades son positivas).
representa
el área bajo la curva de f de modo que la interpretación geométrica de esta
propiedad es sencillamente el área. (También se deduce directamente de la
definición porque todas las cantidades son positivas).
* Si f y g son integrables
en el intervalo cerrado [a, b] con f(x) g(x) para todo x en [a, b] entonces 

Demostración: Si
f(x) g(x) podemos asegurar que f(x) g(x) 0
y le podemos aplicar la propiedad anterior y por lo tanto 


 0 y de esta manera
0 y de esta manera 
Supongamos que m y M son constantes tales que
m f(x) M para a x b.
Se dice que f está acotada arriba por M y acotada abajo por m, la gráfica queda
entre la recta y = m y la recta y =
M. Podemos enunciar el siguiente teorema:
(La
gráfica ilustra la propiedad cuando f(x) 0)
Si y f(x) es continua y m y M son los
valores mínimos y máximos de la misma en el intervalo [a, b] gráficamente esta
propiedad indica que el área debajo de la gráfica de f es mayor que el área del
rectángulo con altura m y menor que la del rectángulo con altura M.
En general dado que m f(x) M
podemos asegurar, por la propiedad anterior que
Si se evalúan las integrales de los extremos
de la desigualdad
SIMETRÍA
El siguiente teorema permite simplificar el
cálculo de integrales de funciones que poseen propiedades de simetría.
Sea f una función continua sobre el intervalo
[–a, a]
En la primera integral sustituimos u –x du –dx,
además si x –a u a.
En el caso a) si la función es par f(–u) f(u)
entonces
Mientras que en el caso b) si la función es impar f(–u) –
f(u)
Ejemplo: Sabiendo
que ,
calcule las siguientes integrales.
,
calcule las siguientes integrales.
 ,
calcule las siguientes integrales.
,
calcule las siguientes integrales.
Utilizando propiedades de las integrales
resulta:
a) Como x2 es una función par:





ÁREA DE
REGIÓN ENTRE DOS CURVAS
Si f y g son dos funciones continuas en [a,
b] y g(x) f(x) x [a, b], entonces el área de la región
limitada por las gráficas de f y g y las rectas verticales x a
y x b es 

Demostración:
Subdividimos el intervalo [a, b] en n subintervalos cada uno de ancho x
y dibujamos un rectángulo representativo de alto f(xi) g(xi)
donde x está en el i-ésimo intervalo.
Área del rectángulo i [f(xi) g(xi)] x
Sumando las áreas y considerando que el
número de rectángulos tiende a infinito resulta que el área total es
Como f y g son continuas en el intervalo, la
función diferencia f g también los es y el límite existe.
Es importante darse cuenta que la validez de la
fórmula del área depende sólo de que f y g sean continuas y de que g(x) f(x).
Las gráficas de f y g pueden estar situadas de cualquier manera respecto del
eje x.
Integración respecto al eje y
Si algunas regiones están acotadas por curvas
que son funciones de y o bien se pueden trabajar mejor considerando x como
función de y los rectángulos representativos para la aproximación se consideran
horizontales en lugar de verticales. De esta manera, si una región está
limitada por las curvas de ecuaciones x f(y), x g(y),
y c y la recta horizontal y d,
donde f y g son continuas y f(y) g(y) para c y d,
entonces su área resulta  .
.
 .
.Área A
 (en la variable x, se consideran
rectángulos verticales)
(en la variable x, se consideran
rectángulos verticales)donde a y b son las abscisas de dos puntos de intersección adyacentes de las dos curvas o puntos de las rectas fronteras que se especifiquen.
Área A
 (en la variable y, se consideran
rectángulos horizontales)
(en la variable y, se consideran
rectángulos horizontales)
donde c y d son las ordenadas de dos puntos de
intersección adyacentes de las dos curvas o puntos de las rectas fronteras que
se especifiquen.
Aca un video de youtube:
https://www.youtube.com/results?search_query=PROPIEDADES+DE+LA+INTEGRAN+DEFINIDA
https://www.youtube.com/results?search_query=PROPIEDADES+DE+LA+INTEGRAN+DEFINIDA


















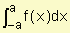








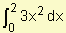


















No hay comentarios.:
Publicar un comentario